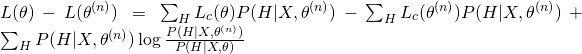Posts

Two important distributions related to Dirichlet distribution

This entry was posted in Topic Model on November 3, 2010 by Liangjie Hong

In this post, we review two important facts of Dirichlet distribution. The basic setting used here as follows. Suppose we have a discrete space $latex \mathcal{X} = \{ \mathcal{X}_{1},\mathcal{X}_{2}, \ldots,\mathcal{X}_{K} \}$. These are $latex K$ outcomes can be observed from the “random experiments”. Suppose we have $latex N$ observations $latex \{X_{1}, X_{2},\ldots, X_{N}\}$ that are distributed according to a Multinomial distribution $latex \theta$ where $latex \theta_{i} = P(X_{j} = \mathcal{X}_{i})$. After placing a Dirichlet distribution $latex \mbox{Dir}(\alpha)$ on $latex \theta$, we are interested in the following two questions:

What is the posterior distribution $P(\theta | \mathbf{X}, \alpha)$ ?
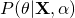What is the predictive distribution $P(X_{N+1} | \mathbf{X}, \alpha)$ ?

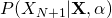Posterior Distribution

We can steadily derive the posterior distribution as below:

$P(\theta | \mathbf{X}, \alpha) = \frac{P(X|\theta)P(\theta|\alpha)}{\int_{\theta} P(X|\theta)P(\theta|\alpha) \, d\theta} \\ = \frac{\Bigr( \prod_{k=1}^{K} (\theta_{k})^{n(k)} \Bigl) \Bigr( \frac{\Gamma(\sum_{k} \alpha_{k})}{\prod_{k} \Gamma(\alpha_{k})} \prod_{k}^{K} \theta_{k}^{\alpha_{k} - 1} \Bigl) }{\int_{\theta} \Bigr( \prod_{k=1}^{K} (\theta_{k})^{n(k)} \Bigl) \Bigr( \frac{\Gamma(\sum_{k} \alpha_{k})}{\prod_{k} \Gamma(\alpha_{k})} \prod_{k}^{K} \theta_{k}^{\alpha_{k} - 1} \Bigl) \, d\theta } \\ = \frac{\Gamma \Bigr( \sum_{k} ( \alpha_{k} + n(k) ) \Bigl)}{\prod_{k}^{K} \Gamma \Bigr( \alpha_{k} + n(k) \Bigl)} \prod_{k}^{K} \theta_{k}^{\alpha_{k} + n(k) -1 }$

where $latex n(k)$ is the number of times outcome $latex \mathcal{X}_{k}$ appear in the data. Therefore, the posterior distribution is indeed a Dirichlet distribution $latex \mbox{Dir} \Bigr( \alpha_{1}+n(1),\alpha_{2}+n(2),\ldots,\alpha_{k}+n(k) \Bigl)$. If we only have one observation $latex X$, this posterior distribution is simply $latex \mbox{Dir} \Bigr( \alpha_{1}+\delta_{1}(X),\alpha_{2}+\delta_{2}(X),\ldots,\alpha_{k}+\delta_{k}(X) \Bigl)$ where $latex \delta_{k}(X)$ is $latex 1$ only if $latex X$ takes the value of outcome $latex \mathcal{X}_{k}$. This notation can also extend to the general case that the posterior distribution is $latex \mbox{Dir} \Bigr( \alpha_{1}+\sum_{i}^{N} \delta_{1}(X_{i}),\alpha_{2}+\sum_{i}^{N} \delta_{2}(X_{i}),\ldots,\alpha_{k}+\sum_{i}^{N} \delta_{k}(X_{i}) \Bigl)$.

Predictive Distribution

By using the posterior distribution derived above, we can have the predictive distribution as follows:

$P(X_{N+1} = \mathcal{X}_{i} | \mathbf{X}, \alpha) = \int_{\theta} P(X_{N+1} = \mathcal{X}_{i} | \theta) P(\theta | \mathbf{X}, \alpha) \, d\theta \\ =\int_{\theta} \theta_{i} \Biggr[ \frac{\Gamma \Bigr( \sum_{k} ( \alpha_{k} + n(k) ) \Bigl)}{\prod_{k}^{K} \Gamma \Bigr( \alpha_{k} + n(k) \Bigl)} \prod_{k}^{K} \theta_{k}^{\alpha_{k} + n(k) -1 } \Biggl] \, d\theta \\ = \mathbb{E}[\theta_{i}] \\ = \frac{\alpha_{i} + n(i)}{\sum_{k} \Bigr( \alpha_{k} + n(k) \Bigl)} = \frac{\alpha_{i} + \sum_{j}^{N} \delta_{i}(X_{j})}{\sum_{k} \alpha_{k} + N }$

where the second last line is derived by observing that the posterior distribution is a Dirichlet distribution and the expression is essentially an expectation under that distribution. Note, the final line of the equation can be re-written into:

$\frac{\alpha_{i} + \sum_{j}^{N} \delta_{i}(X_{j})}{\sum_{k} \alpha_{k} + N } = \Bigr( \frac{\alpha_{i}}{\sum_{k} \alpha_{k}} \Bigl) \Bigr( \frac{\sum_{k} \alpha_{k}}{\sum_{k} \alpha_{k} + N} \Bigl) + \Bigr( \frac{1}{N} \sum_{j}^{N} \delta_{i}(X_{j}) \Bigl) \Bigr( \frac{N}{\sum_{k}\alpha_{k} + N }\Bigl)$

It is the weighted summation of prior mean of $latex \theta_{i}$ and the MLE of $latex \theta_{i}$. There is one extreme case for predictive distribution, which is that there is no data points before. By using the equation we derive above, we have:

$P(X_{N+1} = \mathcal{X}_{i} | \alpha) = \frac{\alpha_{i}}{\sum_{k} \alpha_{k}}$

These two distributions are heavily used in Dirichlet/Multinomial Bayesian modeling and also are milestones for understanding Dirichlet Process.

Notes on Language Models (1)

This entry was posted in IR on January 6, 2010 by Liangjie Hong

[toc]

Query Likelihood Language Models

The basic idea behind Query Likelihood Language Models (QLLM) is that a query is a sample drawn from a language model. In other words, we want to compute the likelihood, that given a document language model $\theta_{D}$ , how likely the posed query $Q$ would be used. Formally, this can be expressed as $P(Q|\theta_{D})$ . Two questions will immediately arise following this formulation. (1) How to choose the model to represent $\theta_{D}$ ? (2) How to estimate $\theta_{D}$ ?

Multinomial Language Model

One popular choice for $\theta_{D}$ is multinomial distribution. The original multinomial distribution is

$P(X_{1}=x_{1},X_{2}=x_{2},\ldots,X_{n}=x_{n})=\frac{n!}{x_{1}!x_{2}!,\ldots,x_{n}!}p_{1}^{x_{1}}p_{2}^{x_{2}},\ldots, p_{n}^{x_{n}}$

In Language Modeling, we usually ignore the coefficient and therefore we obtain unigram language model so that the order of text sequence is not important. Use multinomial distribution to model $\theta_{D}$ , we obtain

$P(Q|\theta_{D}) = \prod_{w \in Q} P(w | \theta_{D}) =\prod_{w \in V} P(w | \theta_{D})^{c(w,Q)}$

where $c(w,Q)$ is the number of times that term $w$ appearing in query $Q$ . Now, the problem becomes to estimate $P(w|\theta_{D})$ . In theory, we need to estimate it for all the terms in our vocabulary. However, since $c(w,Q)$ could be $0$ (meaning that term $w$ does not show up in the query), we only care about the terms in the query.

The key point here is that we do not know $\theta_{D}$ }! How can we calculate $P(w|\theta_{D})$ for the terms in the query when we really do not have a model in hand? One way is to use document $D$ as a sample to estimate $\theta_{D}$ . Therefore, essentially, we choose the model $\theta_{D}$ such that $\hat{\theta_{D}}= arg max_{\theta} P(D|\theta)$ .

One simple way to estimate $P(D|\theta)$ is through Maximum Likelihood Estimator (ML). Now, let us to derive ML for Multinomial Language Model. First, we usually work on log-likelihood rather than the product of probabilities just to avoid very small numbers: $\log P(D|\theta) = \sum_{w \in V} c(w,D) \log P(w|\theta)$ . Then, use Lagrange Multiplers, we obtain:

$L =\log P(D|\theta) + \lambda (1-\sum_{w \in V} P(w|\theta))$

Take all derivatives respect to $P(w|\theta)$ and $\lambda$ :

$\frac{\partial L}{\partial P(w|\theta)} = \frac{c(w,D)}{P(w|\theta)}-\lambda = 0$
$\frac{\partial L}{\partial \lambda } = 1 - \sum_{w \in V} P(w|\theta) = 0$

From the first equation, we can get $P(w|\theta) = \frac{c(w,D)}{\lambda}$ and also $\sum_{w \in V} c(w,D) = \lambda \sum_{w \in V} P(w|\theta)=1$ . Therefore,

$P(w|\theta) = \frac{c(w,D)}{\sum_{w \in V} c(w,D)} =\frac{c(w,D)}{|D|}$

Notes on Probabilistic Latent Semantic Analysis (PLSA) 1

This entry was posted in Topic Model on January 4, 2010 by Liangjie Hong

PLEASE NOTE: THIS PAGE IS AND WILL NOT GET UPDATED.

I highly recommend you read the more detailed version of http://arxiv.org/abs/1212.3900

Formulation of PLSA

There are two ways to formulate PLSA. They are equivalent but may lead to different inference process.

$P(d,w) = P(d) \sum_{z} P(w|z)P(z|d)$
$P(d,w) = \sum_{z} P(w|z)P(d|z)P(z)$

Let’s see why these two equations are equivalent by using Bayes rule.

$P(z|d) = \frac{P(d|z)P(z)}{P(d)}$
$P(z|d)P(d) =P(d|z)P(z)$
$P(w|z)P(z|d)P(d) =P(w|z)P(d|z)P(z)$
$P(d) \sum_{z} P(w|z)P(z|d) = \sum_{z} P(w|z)P(d|z)P(z)$

The whole data set is generated as (we assume that all words are generated independently):

$D = \prod_{d} \prod_{w} P(d,w)^{n(d,w)}$

The Log-likelihood of the whole data set for (1) and (2) are:

$L_{1} = \sum_{d} \sum_{w} n(d,w) \log [ P(d) \sum_{z} P(w|z)P(z|d) ]$

$L_{2} = \sum_{d} \sum_{w} n(d,w) \log [ \sum_{z} P(w|z)P(d|z)P(z) ]$

EM

For $L_{1}$ or $L_{2}$ , the optimization is hard due to the log of sum. Therefore, an algorithm called Expectation-Maximization is usually employed. Before we introduce anything about EM, please note that EM is only guarantee to find a local optimum (although it may be a global one).

First, we see how EM works in general. As we shown for PLSA, we usually want to estimate the likelihood of data, namely $P(X|\theta)$ , given the paramter $\theta$ . The easiest way is to obtain a maximum likelihood estimator by maximizing $P(X|\theta)$ . However, sometimes, we also want to include some hidden variables which are usually useful for our task. Therefore, what we really want to maximize is $P(X|\theta)=\sum_{z}P(X|z,\theta)P(z|\theta)$ , the complete likelihood. Now, our attention becomes to this complete likelihood. Again, directly maximizing this likelihood is usually difficult. What we would like to show here is to obtain a lower bound of the likelihood and maximize this lower bound.

We need Jensen’s Inequality to help us obtain this lower bound. For any convex function $f(x)$ , Jensen’s Inequality states that :

$\lambda f(x) + (1-\lambda) f(y) \geq f(\lambda x + (1-\lambda) y)$

Thus, it is not difficult to show that :

$E[f(x)] = \sum_{x} P(x) f(x) \geq f(\sum_{x} P(x) x) = f(E[x])$

and for concave functions (like logarithm), it is :

$E[f(x)] \leq f(E[x])$

Back to our complete likelihood, we can obtain the following conclusion by using concave version of Jensen’s Inequality :

$\log \sum_{z}P(X|z,\theta)P(z|\theta)= \log \sum_{z}P(X|z,\theta)P(z|\theta)\frac{q(z)}{q(z)}$
$= \log E[\frac{P(X|z,\theta)P(z|\theta)}{q(z)}]$
$\geq E[\log \frac{P(X|z,\theta)P(z|\theta)}{q(z)}]$

Therefore, we obtained a lower bound of complete likelihood and we want to maximize it as tight as possible. EM is an algorithm that maximize this lower bound through a iterative fashion. Usually, EM first would fix current $\theta$ value and maximize $q(z)$ and then use the new $q(z)$ value to obtain a new guess on $\theta$ , which is essentially a two stage maximization process. The first step can be shown as follows:

$E[\log \frac{P(X|z,\theta)P(z|\theta)}{q(z)}] = \sum_{z} q(z) \log \frac{P(X|z,\theta)P(z|\theta)}{q(z)}$
$= \sum_{z} q(z) \log \frac{P(z|X,\theta)P(X,\theta)}{q(z)}$
$= \sum_{z} q(z) \log P(x,\theta) + \sum_{z} q(z) \log \frac{P(z|X,\theta)}{q(z)}$
$= \log P(x,\theta) - \sum_{z} q(z) \log \frac{q(z)}{P(z|X,\theta)}$
$= \log P(x,\theta) - KL(q(z) || P(z|X,\theta))$

The first term is the same for all $z$ . Therefore, in order to maximize the whole equation, we need to minimize KL divergence between $q(z)$ and $P(z|X,\theta)$ , which eventually leads to the optimum solution of $q(z) = P(z|X,\theta)$ . So, usually for E-step, we use current guess of $\theta$ to calculate the posterior distribution of hidden variable as the new update score. For M-step, it is problem-dependent. We will see how to do that in later discussions.

Another explanation of EM is in terms of optimizing a so-called Q function. We devise the data generation process as $P(X|\theta)=P(X,H|\theta)=P(H|X,\theta)P(X|\theta)$ . Therefore, the complete likelihood is modified as:

$L_{c}(\theta) = \log P(X,H|\theta) = \log P(X|\theta) + \log P(H|X,\theta) = L(\theta) + \log P(H|X,\theta)$

Think about how to maximize $L_{c}(\theta)$ . Instead of directly maximizing it, we can iteratively maximize $L_{c}(\theta^{(n+1)})-L_{c}(\theta^{(n)})$ as :

$L(\theta) - L(\theta^{(n)}) = L_{c}(\theta) - \log P(H|X,\theta) - L_{c}(\theta^{(n)}) + \log P(H|X,\theta^{(n)})$
$= L_{c}(\theta) - L_{c}(\theta^{(n)}) + \log \frac{P(H|X,\theta^{(n)})}{P(H|X,\theta)}$

Now take the expectation of this equation, we have:

$L(\theta) - L(\theta^{(n)}) = \sum_{H} L_{c}(\theta)P(H|X,\theta^{(n)}) - \sum_{H} L_{c}(\theta^{(n)})P(H|X,\theta^{(n)}) + \sum_{H} P(H|X,\theta^{(n)})\log \frac{P(H|X,\theta^{(n)})}{P(H|X,\theta)}$

The last term is always non-negative since it can be recognized as the KL-divergence of $P(H|X,\theta^{(n)}$ and $P(H|X,\theta)$ . Therefore, we obtain a lower bound of Likelihood :

$L(\theta) \geq \sum_{H} L_{c}(\theta)P(H|X,\theta^{(n)}) + L(\theta^{(n)}) - \sum_{H} L_{c}(\theta^{(n)})P(H|X,\theta^{(n)})$

The last two terms can be treated as constants as they do not contain the variable $\theta$ , so the lower bound is essentially the first term, which is also sometimes called as “Q-function”.
$Q(\theta;\theta^{(n)}) = E(L_{c}(\theta)) = \sum_{H} L_{c}(\theta) P (H|X,\theta^{(n)})$

EM of Formulation 1

In case of Formulation 1, let us introduce hidden variables $R(z,w,d)$ to indicate which hidden topic $z$ is selected to generated $w$ in $d$ ( $\sum_{z} R(z,w,d) = 1$ ). Therefore, the complete likelihood can be formulated as :

$L_{c1} = \sum_{d} \sum_{w} n(d,w) \sum_{z} R(z,w,d) \log [ P(d) P(w|z)P(z|d) ]$
$= \sum_{d} \sum_{w} n(d,w) \sum_{z} R(z,w,d) [ \log P(d) + \log P(w|z) + \log P(z|d) ]$

From the equation above, we can write our Q-function for the complete likelihood $E[L_{c1}]$ :

$E[L_{c1}] = \sum_{d} \sum_{w} n(d,w) \sum_{z} P(z|w,d) [ \log P(d) + \log P(w|z) + \log P(z|d) ]$

For E-step, simply using Bayes Rule, we can obtain:

$P(z|w,d) = \frac{P(w|z,d)}{P(w,d)}$
$= \frac{P(w|z)P(z|d)P(d)}{\sum_{z} P(w|z)P(z|d)P(d)}$
$= \frac{P(w|z)P(z|d)}{\sum_{z} P(w|z)P(z|d)}$

For M-step, we need to maximize Q-function, which needs to be incorporated with other constraints:

$H = E[L_{c1}]+ \alpha [1-\sum_{d} P(d) ]+ \beta \sum_{z}[1- \sum_{w} P(w|z)]$
$+\gamma \sum_{d}[1- \sum_{z} P(z|d)]$

and take all derivatives:

$\frac{\partial H}{\partial P(d)} = \sum_{w} \sum_{z} n(d,w) \frac{P(z|w,d)}{P(d)} - \alpha = 0$
$\rightarrow \sum_{w} \sum_{z} n(d,w) P(z|w,d) - \alpha P(d) = 0$
$\frac{\partial H}{\partial P(w|z)} = \sum_{d} n(d,w) \frac{P(z|w,d)}{P(w|z)} - \beta = 0$
$\rightarrow \sum_{d} n(d,w) P(z|w,d) - \beta P(w|z) = 0$
$\frac{\partial H}{\partial P(z|d)} = \sum_{w} n(d,w) \frac{P(z|w,d)}{P(z|d)} - \gamma = 0$
$\rightarrow \sum_{w} n(d,w) P(z|w,d) - \gamma P(z|d) = 0$

Therefore, we can easily obtain:

$P(d) = \frac{\sum_{w} \sum_{z} n(d,w) P(z|w,d)}{\sum_{d} \sum_{w} \sum_{z} n(d,w) P(z|w,d)}$
$= \frac{n(d)}{\sum_{d} n(d)}$
$P(w|z) = \frac{\sum_{d} n(d,w) P(z|w,d)}{\sum_{w} \sum_{d} n(d,w) P(z|w,d) }$
$P(z|d) = \frac{\sum_{w} n(d,w) P(z|w,d)}{\sum_{z} \sum_{w} n(d,w) P(z|w,d) }$
$= \frac{\sum_{w} n(d,w) P(z|w,d)}{n(d)}$

EM of Formulation 2

Use similar method to introduce hidden variables to indicate which $z$ is selected to generated $w$ and $d$ and we can have the following complete likelihood :

$L_{c2} = \sum_{d} \sum_{w} n(d,w) \sum_{z} R(z,w,d) \log [ P(z) P(w|z)P(d|z) ]$
$= \sum_{d} \sum_{w} n(d,w) \sum_{z} R(z,w,d) [ \log P(z) + \log P(w|z) + \log P(d|z) ]$

Therefore, the Q-function $E[L_{c2}]$ would be :

$E[L_{c2}] = \sum_{d} \sum_{w} n(d,w) \sum_{z} P(z|w,d) [ \log P(z) + \log P(w|z) + \log P(d|z) ]$

For E-step, again, simply using Bayes Rule, we can obtain:

$P(z|w,d) = \frac{P(w|z,d)}{P(w,d)}$
$= \frac{P(w|z)P(d|z)P(z)}{\sum_{z} P(w|z)P(d|z)P(z)}$

For M-step, we maximize the constraint version of Q-function:

$H = E[L_{c2}] + \alpha [1-\sum_{z} P(z) ] + \beta \sum_{z}[1- \sum_{w} P(w|z)]+$
$+\gamma \sum_{z} [1- \sum_{d} P(d|z)]$

and take all derivatives:

$\frac{\partial H}{\partial P(z)}= \sum_{d} \sum_{w} n(d,w) \frac{P(z|w,d)}{P(z)} - \alpha = 0$
$\rightarrow \sum_{d} \sum_{w} n(d,w) P(z|w,d) - \alpha P(z)= 0$

$[latex]\rightarrow \sum_{d} n(d,w) P(z|w,d) - \beta P(w|z) = 0$

$\frac{\partial H}{\partial P(d|z)} = \sum_{w} n(d,w) \frac{P(z|w,d)}{P(d|z)} - \gamma = 0$
$\rightarrow \sum_{w} n(d,w) P(z|w,d) - \gamma P(d|z) = 0$

Therefore, we can easily obtain:

$P(z) = \frac{\sum_{d} \sum_{w} n(d,w) P(z|w,d)}{\sum_{d} \sum_{w} \sum_{z} n(d,w) P(z|w,d)}$
$= \frac{\sum_{d} \sum_{w} n(d,w) P(z|w,d)}{\sum_{d} \sum_{w} n(d,w)}$
$P(w|z)= \frac{\sum_{d} n(d,w) P(z|w,d)}{\sum_{w} \sum_{d} n(d,w) P(z|w,d) }$
$P(d|z) = \frac{\sum_{w} n(d,w) P(z|w,d)}{\sum_{d} \sum_{w} n(d,w) P(z|w,d) }$