There is a trend in research communities to bring two well-established classes of models together, topic models and latent factor models. By doing so, we may enjoy the ability to analyze text information with topic models and incorporate the collaborative filtering analysis with latent factor models. In this section, I wish to discuss some of these efforts.
Three papers will be covered in this post are listed at the end of the post. Before that, let’s first review what latent factor models are. Latent factor models (LFM) are usually used in collaborative filtering context. Say, we have a user-item rating matrix  where
where 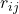 represents the rating user
represents the rating user 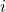 gives to item
gives to item 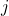 . Now, we assume for each user
. Now, we assume for each user 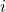 , there is a vector
, there is a vector 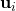 with the dimensionality
with the dimensionality 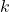 , representing the user in a latent space. Similarly, we assume for each item
, representing the user in a latent space. Similarly, we assume for each item 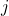 , a vector
, a vector 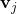 with the same dimensionality representing the item in a same latent space. Thus, the rating
with the same dimensionality representing the item in a same latent space. Thus, the rating 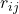 is therefore represented as:
is therefore represented as:
![Rendered by QuickLaTeX.com \[ r_{ij} = \mathbf{u}_{i}^{T} \mathbf{v}_{j} \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-79a64e02acfa4a63e35c77381edb0083_l3.png)
This is the basic setting for LFM. In addition to this basic setting, additional biases can be incorporated, see here. For topic models (TM), the simplest case is Latent Dirichlet Allocation (LDA). The story of LDA is like this. For a document 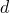 , we first sample a multinomial distribution
, we first sample a multinomial distribution 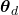 , which is a distribution over all possible topics. For each term position
, which is a distribution over all possible topics. For each term position 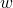 in the document, we sample a discrete topic assignment
in the document, we sample a discrete topic assignment  from
from 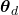 , indicating which topic we use for this term. Then, we sample a term
, indicating which topic we use for this term. Then, we sample a term  from a topic
from a topic 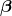 , a multinomial distribution over the vocabulary.
, a multinomial distribution over the vocabulary.
For both LFM and TM, they are methods to reduce original data into latent spaces. Therefore, it might be possible to link them together. Especially, items in the LFM are associated with rich text information. One natural idea is that, for an item 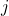 , the latent factor
, the latent factor 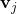 and its topic proportional parameter
and its topic proportional parameter 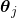 somehow gets connected. One way is to directly equalize these two variables. Since
somehow gets connected. One way is to directly equalize these two variables. Since 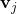 is a real-value variable and
is a real-value variable and 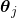 falls into a simplex, we need certain ways to keep these properties. Two possible methods can be used:
falls into a simplex, we need certain ways to keep these properties. Two possible methods can be used:
- Keep
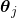 and make sure it is in the range of [0, 1] in the optimization process. Essentially put some constraint on the parameter.
and make sure it is in the range of [0, 1] in the optimization process. Essentially put some constraint on the parameter. - Keep
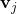 and use logistic transformation to transfer a real-valued vector into simplex.
and use logistic transformation to transfer a real-valued vector into simplex.
Hanhuai and Banerjee showed the second technique in their paper by combining Correlated Topic Model with LFM. Wang and Blei argued that this setting suffers from the limitation that it cannot distinguish topics for explaining recommendations from topics important for explaining content since the latent space is strictly equal. Thus, they proposed a slightly different approach. Namely, each 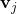 derives from
derives from 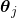 with item-dependent noise:
with item-dependent noise:
![Rendered by QuickLaTeX.com \[ \mathbf{v}_{j} = \boldsymbol{\theta}_{j} + \epsilon_{j} \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-1b58f965a2d3e68c4190d43b239143f6_l3.png)
where 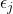 is a Gaussian noise.
is a Gaussian noise.
A different approach is to not directly equal these two quantities but let me impact these each other. One such way explored by Hanhuai and Banerjee is that 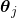 influences how
influences how 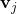 is generated. More specifically, in Probabilistic Matrix Factorization (PMF) setting, all
is generated. More specifically, in Probabilistic Matrix Factorization (PMF) setting, all 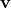 s are generated by a Gaussian distribution with a fixed mean and variance. Now, by combining LDA, the authors allow different topic has different Gaussian prior mean and variance values. A value similar to
s are generated by a Gaussian distribution with a fixed mean and variance. Now, by combining LDA, the authors allow different topic has different Gaussian prior mean and variance values. A value similar to  is firstly generated from
is firstly generated from 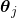 to decide which mean to use and then generate
to decide which mean to use and then generate 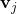 from that particular mean and variance.
from that particular mean and variance.
A totally different direction was taken by Agarwal and Chen. In their fLDA paper, there is no direct relationship between item latent factor and content latent factor. In fact, their relationship is realized by the predictive equation:
![Rendered by QuickLaTeX.com \[ r_{ij} = \mathbf{a}^{T} \mathbf{u}_{i} + \mathbf{b}^{T} \mathbf{v}_{j} + \mathbf{s}_{i}^{T} \bar{\mathbf{z}}_{j}\]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-4e4a57881e426d5425100935dc4d14ff_l3.png)
where 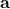 ,
, 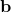 and
and 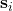 are regression weights and
are regression weights and 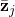 is the average topic assignments for item
is the average topic assignments for item 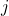 . Note,
. Note, 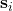 is a user-dependent regression weights. This formalism encodes the notion that all latent factors (including content) will contribute to the rating, not only item and user factors.
is a user-dependent regression weights. This formalism encodes the notion that all latent factors (including content) will contribute to the rating, not only item and user factors.
In summary, three directions have been taken for integrating TM and LFM:
- Equal item latent factor and topic proportion vector, or make some Gaussian noise.
- Let topic proportion vector to control the prior distribution for item latent factor.
- Let item latent factor and topic assignments, as well as user latent factor, contribute the rating.
Reference:
- Deepak Agarwal and Bee-Chung Chen. 2010. fLDA: matrix factorization through latent dirichlet allocation. In Proceedings of the third ACM international conference on Web search and data mining (WSDM ’10). ACM, New York, NY, USA, 91-100. [PDF]
- Hanhuai Shan and Arindam Banerjee. 2010. Generalized Probabilistic Matrix Factorizations for Collaborative Filtering. In Proceedings of the 2010 IEEE International Conference on Data Mining (ICDM ’10). IEEE Computer Society, Washington, DC, USA, 1025-1030. [PDF]
- Chong Wang and David M. Blei. 2011. Collaborative topic modeling for recommending scientific articles. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD ’11). ACM, New York, NY, USA, 448-456.[PDF]

![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (1) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-26f49852a50c1f981273da59a3d7de67_l3.png" height="213" width="233" class="ql-img-displayed-equation " alt="\begin{eqnarray*}P(-x) &=& \frac{1}{1+\exp(x)} \nonumber \\&=& \frac{1}{1+\frac{1}{\exp(-x)}} \nonumber \\&=& \frac{\exp(-x)}{1+\exp(-x)} \nonumber \\&=& 1 - \frac{1}{1+\exp(-x)} \nonumber \\&=& 1 - P(x) \; \; \qquad (2)\end{eqnarray*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-42d346a397a5ef77a0c95da4f9c5ceb9_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (2) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-0d2ec58cfdefbc85b337c9195b7e9d47_l3.png" height="96" width="333" class="ql-img-displayed-equation " alt="\begin{eqnarray*}P(y = 1 \, | \, \boldsymbol{\beta}, \mathbf{x}) &=& \frac{\exp(\boldsymbol{\beta}^{T} \mathbf{x})}{1 + \exp(\boldsymbol{\beta}^{T} \mathbf{x})} \nonumber \\P(y = 0 \, | \, \boldsymbol{\beta}, \mathbf{x}) &=& \frac{1}{1 + \exp(\boldsymbol{\beta}^{T} \mathbf{x})} \;\; \qquad (3)\end{eqnarray*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-9a74f66d1bb17a71c128557f173bd7e0_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (3) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-ab78efd52d92fe6f7a6a48a6387e0bce_l3.png" height="19" width="276" class="ql-img-displayed-equation " alt="\begin{equation*}P(y=1 \, | \, \boldsymbol{\beta}, \mathbf{x}) = 1 - P(y=0 \, | \, \boldsymbol{\beta}, \mathbf{x})\end{equation*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-18581b7919baa6007aacf245b60a1972_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (4) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-adce25678a6ba44c60e8e18024431334_l3.png" height="43" width="347" class="ql-img-displayed-equation " alt="\begin{equation*}P(g= \pm 1 \, | \, \boldsymbol{\beta}, \mathbf{x}) = \frac{1}{1 + \exp( - g\boldsymbol{\beta}^{T} \mathbf{x})} \;\; \qquad (4)\end{equation*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-55c297fcdaba8e509f70fdfa37302b5d_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (5) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-e86023543d98b569af5f56638c5993ff_l3.png" height="175" width="278" class="ql-img-displayed-equation " alt="\begin{eqnarray*}P(y = 1 \, | \, \boldsymbol{\beta}, \mathbf{x}) &=& \frac{\exp(\boldsymbol{\beta}^{T} \mathbf{x})}{1 + \exp(\boldsymbol{\beta}^{T} \mathbf{x})} \nonumber \\&=& \frac{1}{\frac{1}{\exp(\boldsymbol{\beta}^{T} \mathbf{x})} + 1} \nonumber \\&=& \frac{1}{\exp(-\boldsymbol{\beta}^{T} \mathbf{x}) + 1} \nonumber \\&=& P(g= 1 \, | \, \boldsymbol{\beta}, \mathbf{x})\end{eqnarray*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-4ddd8c95a47dad31270f1962ba10f5ac_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (6) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-bb3dda211fa7695381356592f2eac0f8_l3.png" height="117" width="225" class="ql-img-displayed-equation " alt="\begin{eqnarray*}\frac{\frac{\exp(\boldsymbol{\beta}^{T} \mathbf{x})}{1 + \exp(\boldsymbol{\beta}^{T} \mathbf{x})}}{\frac{1}{1 + \exp(\boldsymbol{\beta}^{T} \mathbf{x})}} & > & 1 \;\; \rightarrow \;\; y = 1 \nonumber \\\exp(\boldsymbol{\beta}^{T} \mathbf{x}) & > & 1 \nonumber \\\boldsymbol{\beta}^{T} \mathbf{x} & > & 0\end{eqnarray*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-8c6bba07a730a338dab0793007011abb_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (7) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-110b1c3ae6ac1d5eeddfaffa87acae4c_l3.png" height="166" width="264" class="ql-img-displayed-equation " alt="\begin{eqnarray*}\frac{\frac{1}{1 + \exp( - \boldsymbol{\beta}^{T} \mathbf{x})}}{\frac{1}{1 + \exp( \boldsymbol{\beta}^{T} \mathbf{x})}} & > & 1 \;\; \rightarrow \;\; g = 1 \nonumber \\\frac{1 + \exp(\boldsymbol{\beta}^{T} \mathbf{x})}{1 + \exp( - \boldsymbol{\beta}^{T} \mathbf{x})} & > & 1 \nonumber \\\exp(\boldsymbol{\beta}^{T} \mathbf{x}) & > & 1 \nonumber \\\boldsymbol{\beta}^{T} \mathbf{x} & > & 0\end{eqnarray*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-9ad0644e968541888a1a3d6ad55a5d3f_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (8) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-7b2ccccdd2c250978dabe7bef0c428ee_l3.png" height="42" width="183" class="ql-img-displayed-equation " alt="\begin{equation*}\arg\min \sum_{i} L\Bigr(y_{i},f(\mathbf{x}_{i})\Bigl)\end{equation*}" title="Rendered by QuickLaTeX.com"/>\]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-df99f36ed6aedb2edb3f330175f08294_l3.png)
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> (9) </span><span class="ql-left-eqno"> </span><img src="https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-38105dc931573fa3c94d601dccba3b8a_l3.png" height="59" width="296" class="ql-img-displayed-equation " alt="\begin{eqnarray*}f(\mathbf{x}) &=& \boldsymbol{\beta}^{T} \mathbf{x} \nonumber \\L\Bigr(y,f(\mathbf{x})\Bigl) &=& \log \Bigr( 1 + \exp(-y f(\mathbf{x})\Bigl)\end{eqnarray*}" title="Rendered by QuickLaTeX.com"/>\]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-262ad5197f16fece83b161c03c7c6803_l3.png)
![Rendered by QuickLaTeX.com \[P(c_{n} = k | \mathbf{c}_{1:n-1}) = \begin{cases}\frac{m_{k}}{n-1+\alpha}, & \mbox{if } k \leq \mathbf{K}_{+} \mbox{ (i.e., $k$ is a previously occupied table)} \\\frac{\alpha}{n-1+\alpha}, & \mbox{otherwise (i.e., $k$ is the next unoccupied table)}\end{cases}\]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-da195e11008721383f496cbe4a35f65f_l3.png)
![Rendered by QuickLaTeX.com \[ p(c_{1}, c_{2}, \cdots , c_{N}) = \prod_{k=1}^{K} \frac{\alpha (N_{k}-1)!}{(I_{k,1}-1+\alpha)(I_{k,2}-1+\alpha)\cdots (I_{k,N_{k}}-1+\alpha)} \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-442b2b90242f1dda0a7bb7fd918745c7_l3.png)
![Rendered by QuickLaTeX.com \[ p(c_{1}, c_{2}, \cdots , c_{N}) = \frac{\alpha^{K} \prod_{k=1}^{K} (N_{k}-1)! }{\prod_{i=1}^{N} (i-1+\alpha)} \]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-d08ffdaf6fd4cf68471e63d2dba97462_l3.png)