Research in General

Smoothing Techniques for Complex Relationships between Probability Distributions

This entry was posted in Research in General on by

Imagine you want to estimate the probability of how likely a user u in San Francisco would click on a particular news article i. We represent this probability as P(a_{i} =1 \, | \, u) where a_{i} is a binary variable for article i to encode whether the user clicks on it or not. The simplest way to estimate such probability is to stick to Maximum Likelihood Estimation (MLE) where P can be easily computed as:

(1)   \begin{equation*}P( a_{i} = 1 \, | \, u ) = \frac{C(i,u)}{N(i,u)}\end{equation*}

where C(i,u) is the number of times user u clicks on article i and N(i,u) is the number of times article i is shown to the user u.

Everything works fine until we face a new article, let’s say j, that has never shown to the user before. In this case, C(j, u) is effectively zero and we could show the article to the user a couple of times, in hoping of gathering a couple of clicks. However, this is not guaranteed. Moreover, we should be able to estimate P before showing to the user where N is also zero!

In statistical modeling, a common practice for the situation mentioned above is to impose a prior distribution over P where pseudo counts are added to C and N, yielding non-zero ratio of the Equation \eqref{eq:mle}. For example, one could specify a Beta distribution over P where the posterior distribution is another Beta distribution, making the inference straightforward. A thorough study on how these smoothing techniques applying to Information Retrieval has been intensively explored in [1].

The smoothing scenario becomes complicated when multiple related probability distributions get involved. For instance, instead of just estimating how likely a user would click on an article in general, you would be interested in estimating how likely a user would click an article in a particular time of day (e.g., morning or night), or in a particular geographical location (e.g., coffee shop) like P( a_{i}=1 \, | \, u, t ) or P( a_{i} = 1 \, | \, u, g ) where t and g represent a particular context. Of course, we could use MLE again to infer these probabilities but, in general, they will suffer from even severe data sparsity issues and stronger and smarter smoothing techniques are required.

Given related probabilities like P (a_{i} = 1 \, | \, u ), P( a_{i}=1 \, | \, u, t ) and P( a_{i} = 1 \, | \, u, g ), it is not straightforward to define a hierarchical structure to impose a prior distribution over all these distributions. The general idea would be that, they should be smoothed over each other altogether.

Traditionally, smoothing over a complex structure, or usually, when the structure can be defined as a graph, is a well-studied sub-area of machine learning called Graph-based Semi-Supervised Learning (SSL). Good references are like [2,3]. One example of how such algorithms can be applied to probability distributions is [4]. In general, we perform the following two steps to conduct SSL:

  1. Construct a graph for quantities we care about, in this case, they are probability distributions.
  2. Perform a specific form of label propagation on the graph, resulting in a stationary values of quantities we care about.

However, one critical issue with [2,3,4] is that, the fundamental algorithm is designed based on square errors, assuming Gaussian models underneath, which is not appropriate for probability distributions.

A recently proposed framework nicely tackled the problem mentioned above [5], which is to learn probability distributions over a graph. Let’s list the main framework from the paper:

(2)   \begin{equation*}\mathcal{C}_{KL} = \sum_{i=1}^{l} D_{KL} (r_{i} || p_{i}) + \mu \sum_{i=1}^{m} \sum_{j \in \mathcal{N}_{i}} w_{ij} D_{KL}(p_{i} || p_{j}) - \nu \sum_{i=1}^{m}H(p_{i})\end{equation*}

where r_{i} is the original probability distributions, p_{i} is the smoothed probability distribution, D_{KL} is the standard KL divergence between two distributions and H is Shannon entropy. Here, \mu and \nu are two hyper-parameters. l is the number of labeled nodes, m is the number of all nodes. Equation \eqref{eq:kl} is a general framework to learn distributions over labeled and unlabeled nodes. The first term imposes the closeness between smoothed version and the original version of distributions and the second term is the smoothness over the neighborhood graph and the third term is to penalize shape distributions, encouraging uniform distributions.

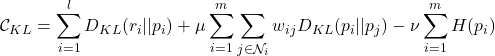
In paper [5], the authors proposed alternative minimization techniques and also mentioned methods of multipliers to solve the problem.

Reference

  1. Chengxiang Zhai and John Lafferty. 2001. A study of smoothing methods for language models applied to ad-hoc information retrieval. In Proceedings of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’01). ACM, New York, NY, USA, 334-342.
  2. D. Zhou, O. Bousquet, T.N. Lal, J. Weston and B. Schölkopf. Learning with Local and Global Consistency. Advances in Neural Information Processing Systems (NIPS) 16, 321-328. (Eds.) S. Thrun, L. Saul and B. Schölkopf, MIT Press, Cambridge, MA, 2004.
  3. Xiaojin Zhu, Zoubin Ghahramani, and John Lafferty. Semi-supervised learning using Gaussian fields and harmonic functions. In The 20th International Conference on Machine Learning (ICML), 2003.
  4. Qiaozhu Mei, Duo Zhang, and ChengXiang Zhai, A General Optimization Framework for Smoothing Language Models on Graph Structures. in Proceedings of the 31th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’08), pp. 611-618, 2008.
  5. Amarnag Subramanya and Jeff Bilmes. 2011. Semi-Supervised Learning with Measure Propagation. The Journal of Machine Learning Research 12 (November 2011), 3311-3370.

Unbiased Offline Evaluation Process of Contextual Multi-armed Bandit Models 2

This entry was posted in Research in General on by

In this post, I would like to discuss some strategies to evaluate contextual multi-armed bandit (cMAB) models in an unbiased offline evaluation setting. The setting is not only applicable for cMAB models but also can be served as a standard process for any machine learning models from online feedback data.

Review of Contextual Multi-armed Bandit Problems

A cMAB problem is a sequential decision making process. Bandit problems invovle making a decision in each round. Once a decision is made an observation is collected and the corresponding reward computed. The contextual-bandit formalism generalizes this classic setting by introducing contextual information in the interaction loop.

Formally, we define by \mathcal{A} = \{1,2,\cdots, K\}, a set of actions, a contextual vector \mathbf{x}_{t} \in \mathcal{X}, a reward vector \mathbf{r}_{t} = \{\mathbf{r}_{t,1}, \cdots, \mathbf{r}_{t,K}\}, where each \mathbf{r}_{t,a} \in [0,1] and a policy \pi : \mathcal{X} \rightarrow \mathcal{A}. A contextual bandit describes a round-by-round interaction between a learner and the environment. At each round t, the problem can be decomposed into following steps:

  • The environment chooses (\mathbf{x}_{t}, \mathbf{r}_{t}) from some unknown distribution \mathbb{D}. Only \mathbf{x}_{t} is revealed to the learner while the reward is not.
  • Upon observing \mathbf{x}_{t}, the learner uses some policy \pi to choose an action a \in \mathcal{A}, and in return observes the corresponding reward \mathbf{r}_{t,a}.
  • (Optional) The policy \pi is revised with the data collected for this round.

Here, we define \pi is parameterized by an unknown parameter \theta. Ideally, we would like to choose the policy maximizing the expected reward:

    \begin{align*}\arg\max_{\pi} \mathbb{E}_{\mathbf{x}, \mathbf{r} \sim \mathcal{D}} \Bigr[ \mathbf{r}_{\pi(\mathbf{x};\theta)}\Bigl]\end{align*}

An important fact in cMAB is that, only rewards of the chosen actions are observed. An online learning must therefore find a good balance between exploration and exploitation, a challenge in bandit problems. For offline policy evaluation, such partial observation raises even further difficulties. Data in a contextual bandit is often in the form of \mathbf{x}, a, \mathbf{r}_{a}, where a is the action chosen for context x when collecting the data, and \mathbf{r}_{a} is the corresponding reward. If this data is used to evaluate policy \pi, which chooses a different action \pi(x) \neq a, then we simply do not have the reward signal to evaluate the policy in that context.

Policy Evaluation

In order to evaluate different policies in an unbiased environment, we need to gather data using a logging policy. This policy is specially designed such that the data can be re-use for offline evaluation. As pointed out in [1], a randomized data collection, which has been known to be critical condition for drawing valid causal conclusions. From [1], the authors proposed the following data collection procedure. At each round,

  • Environment chooses \mathbf{x}, \mathbf{r}, i.i.d. from some unknown distribution \mathbb{D}, and only reveals context \mathbf{x}.
  • Based on x, one compute a multinomial distribution \mathbf{p} over the actions \mathcal{A}. A random action a is drawn according to the distribution, and the corresponding reward \mathbf{r}_{a} and probability mass \mathbf{p}_{a} are logged. Note that \mathbf{p} may depend on \mathbf{x}.

A key point here is that, rather than choosing the optimal action at each round, we would like to choose a random action according some distribution over actions. Also, the probability to select such action should be recorded.

At the end of the process, we have a dataset \mathcal{D} containing data of the form ( \mathbf{x}, a, \mathbf{r}_{a}, \mathbf{p}_{a} ). In statistics, the probabilities \mathbf{p}_{a} are also known as propensity scores.

In order evaluate the value of a policy \pi in such dataset, the following estimator is used:

(1)   \begin{align*}\hat{V}_{\mbox{offline}}(\pi) = \sum_{(x,a,\mathbf{r}_{a},\mathbf{p}_{a}) \in \mathcal{D}} \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}}\end{align*}

This evaluation method is also used in [2] and [3].

Unbiased Offline Evaluation

We define the value of a policy \pi as:

(2)   \begin{align*}V(\pi) &= \mathbb{E}_{(x,d) \in \mathbb{D}}\Bigr[ \mathbf{r}_{a} P(\pi(x) = a \, |\, x) \Bigl] \\&= \int_{(x,r) \in \mathbb{D}} \mathbf{r}_{a} P(\pi(x) = a \, |\, x) P(x,r) \, dx dr\end{align*}

When the policy is deterministic, meaning that, given a contextual vector x, the arm a is always chosen, the above value becomes:

(3)   \begin{align*}V(\pi) &= \mathbb{E}_{(x,d) \in \mathbb{D}}\Bigr[ \mathbf{r}_{\pi_{x}} \Bigl] \\&= \int_{(x,r) \in \mathbb{D}} \mathbf{r}_{\pi_{x}} P(x,r) \, dx dr\end{align*}

In both cases, we want to prove:

(4)   \begin{align*}\mathbb{E}_{\mathcal{D} \in \mathbb{D}} \Bigr[ \hat{V}_{\mbox{offline}}(\pi)\Big] = V(\pi)\end{align*}

In the following discussion, we focus on the deterministic case. Let us expand the left hand side as:

(5)   \begin{align*}\int_{\mathcal{D} \in \mathbb{D}} \Bigr[ \sum_{(x,a,\mathbf{r}_{a},\mathbf{p}_{a}) \in \mathcal{D}} \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}} \Bigl] P(\mathcal{D}) \, d\mathcal{D}\end{align*}

The important step in the proof is that we need to make use of the following quantity:

(6)   \begin{align*}\mathbb{E}_{a \in \mathbf{p}} \Bigr[ \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}} \Bigl] = \mathbf{r}_{a} \mathbb{I}(\pi(x) == a) = \mathbf{r}_{\pi(x)} \end{align*}

Thus, on expectation, we have:

(7)   \begin{align*}\int_{\mathcal{D} \in \mathbb{D}} \Bigr[ \sum_{(x,a,\mathbf{r}_{a},\mathbf{p}_{a}) \in \mathcal{D}} \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}} \Bigl] P(\mathcal{D}) \, d\mathcal{D} = \int_{\mathcal{D} \in \mathbb{D}} \Bigr[ \sum_{(x, \mathbf{r}) \in \mathcal{D}} \mathbf{r}_{\pi(x)} \Bigl] P(\mathcal{D}) \, d\mathcal{D}\end{align*}

As (x,r) from \mathcal{D} are sampled from \mathbb{D} i.i.d., \mathcal{D} is a random sample from \mathbb{D}. The integral also mounts to \mathbb{D}. Note that the key part is Equation \eqref{randomarm} we need to select arms stochastically.

References

  1. L. Li, S. Chen, J. Kleban, and A. Gupta. Counterfactual estimation and optimization of click metrics for search engines. Technical Report MSR-TR-2014-32, Microsoft Research, 2014.
  2. L. Li, W. Chu, J. Langford, and X. Wang. Unbiased offline evaluation of contextual-bandit-based news article recommendation algorithms. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, WSDM ’11, pages 297–306, New York, NY, USA, 2011. ACM.
  3. A. L. Strehl, J. Langford, L. Li, and S. Kakade. Learning from logged implicit exploration data. In NIPS, pages 2217–2225, 2010.

Combining Regression and Ranking

This entry was posted in Research in General on by

It would be hard to imagine that we want to combine the regression problems and ranking problems together. They’re inherently different. Traditionally, ranking problems only concern the order of ranked items. Even you could have very bad scores for each item, the final order matters.

However, there’re situations we care both the scores for each item, as well as their order. One would argue that eventually this is a regression problem because if you predict 100% accurate on all items and therefore the order should be correct as well. This is true only if you have a perfect regression model. There’re a lot of cases where you have a nearly perfect regression model but the results are terrible in terms of ranking. For instance, you could have a very imbalanced dataset where the majority class has y=0. Thus, it is possible to achieve a near-perfect regression performance by always predicting 0, which gives a useless ranking.

D. Sculley provided an easy solution to the problem (published on KDD 2010) above. Basically, we just naively combine two problems together as a single optimization problem, balanced by a parameter as

    \[\min_{\mathbf{w} \in \mathbb{R}^{m}} \alpha L(\mathbf{w}, D) + (1-\alpha)L(\mathbf{w}, P) + \frac{\lambda}{2}||\mathbf{w}||^{2}_{2}\]


where \alpha \in [0,1]. The overall optimization problem is solved through Stochastic Gradient Descent (SGD).

The paper also described efficiently sampling from P and other scalability issues.

How to Generate Gamma Random Variables 4

This entry was posted in Practical Programming Research in General on by

In this post, I would like to discuss how to generate Gamma distributed random variables. Gamma random variate has a number of applications. One of the most important application is to generate Dirichlet distributed random vectors, which plays a key role in topic modeling and other Bayesian algorithms.

A good starting point is a book by Kroese et al. [1] where detailed discussion about how to generate a number of different random distributed variables. In the book (Section 4.2.6), they list the following methods for Gamma distribution:

  • Marsaglia and Tsang’s method [2]
  • Ahrens and Dieter’s method [3]
  • Cheng and Feast’s method [4]
  • Best’s method [5]

Here, we focus on Marsaglia and Tsang’s method, which is used in GSL Library and Matlab “gamrnd” command (you can check this by typing “open gamrnd”).

Gamma Distribution

As there are at least two forms of Gamma distribution, we focus the following formalism of PDF:

    \[f(x; \alpha; \beta) = \frac{\beta^{\alpha} x^{\alpha - 1} e^{-\beta x} }{\Gamma(\alpha)}, \,\,\,\, x \geq 0\]

where \alpha > 0 is called the shape parameter and \beta > 0 is called the scale parameter.

Marsaglia and Tsang’s Method

The algorithm works as follows for \mathbf{X} \sim \mbox{Gamma}(\alpha, 1) for \alpha \geq 1:

  1. Set d = \alpha - 1/3 and c = 1/\sqrt{9d}.
  2. Generate Z \sim \mbox{N}(0,1) and U \sim \mbox{U}(0,1) independently.
  3. If Z > -1/c and \log U < \frac{1}{2} Z^{2} + d - d V + d \times ln V, where V = (1+cZ)^{3}, return \mathbf{X} = d \times V; otherwise, go back to Step 2.

Two notes:

  1. This method can be easily extended to the cases where 1 > \alpha > 0. We just generate \mathbf{X} \sim \mbox{Gamma}(\alpha + 1, \beta), then \mathbf{X}^{\prime} = \mathbf{X} \times U^{1/\alpha} where U \sim (0,1). Thus, \mathbf{X}^{\prime} \sim \mbox{Gamma}(\alpha, \beta). See details in Page 9 of [2].
  2. For \beta \neq 1, we firstly generate \mathbf{X} \sim \mbox{Gamma}(\alpha, 1), then \mathbf{X}/\beta \sim \mbox{Gamma}(\alpha, \beta).

Implementations

Here, we discuss some implementations details. We start from the original proposed C code from [2]:

#include 

extern float RNOR; // Normal random variable
extern float UNI;  // Uniform random variable

float rgama(float a) {
  float d, c, x, v, u;
  d = a - 1. / 3.;
  c = 1. / sqrt(9. * d);
  for (;;) {
    do {
      x = RNOR;
      v = 1. + c * x;
    } while (v <= 0.);
    v = v * v * v;
    u = UNI;
    if (u < 1. - 0.0331 * (x * x) * (x * x)) {
      return (d * v);
    }
    if (log(u) < 0.5 * x * x + d * (1. - v + log(v))) {
      return (d * v);
    }
  }
}

which is slightly different from the algorithm proposed above. Again, this does not handle 1 > \alpha > 0 and \beta \neq 1.

This is the Matlab sample code from [1]:

function x=gamrand(alpha,lambda)
% Gamma(alpha,lambda) generator using Marsaglia and Tsang method
% Algorithm 4.33
if alpha>1
    d=alpha-1/3; c=1/sqrt(9*d); flag=1;
    while flag
        Z=randn;
        if Z>-1/c
            V=(1+c*Z)^3; U=rand;
            flag=log(U)>(0.5*Z^2+d-d*V+d*log(V));
        end
    end
    x=d*V/lambda;
else
    x=gamrand(alpha+1,lambda);
    x=x*rand^(1/alpha);
end

This code does everything.

This is the code snippet extracted from GSL library:

double gsl_ran_gamma (const gsl_rng * r, const double a, const double b)
{
  /* assume a > 0 */

  if (a > 1)
    {
      double u = gsl_rng_uniform_pos (r);
      return gsl_ran_gamma (r, 1.0 + a, b) * pow (u, 1.0 / a);
    }

  {
    double x, v, u;
    double d = a - 1.0 / 3.0;
    double c = (1.0 / 3.0) / sqrt (d);

    while (1)
      {
        do
          {
            x = gsl_ran_gaussian_ziggurat (r, 1.0);
            v = 1.0 + c * x;
          }
        while (v >= 0);

        v = v * v * v;
        u = gsl_rng_uniform_pos (r);

        if (u > 1 - 0.0331 * x * x * x * x) 
          break;

        if (log (u) > 0.5 * x * x + d * (1 - v + log (v)))
          break;
      }

    return b * d * v;
  }
}

Again, this does everything. Note this code is based on a slightly different PDF: {1 \over \Gamma(a) b^a} x^{a-1} e^{-x/b}.

Reference

[1] D.P. Kroese, T. Taimre, Z.I. Botev. Handbook of Monte Carlo Methods. John Wiley & Sons, 2011.
[2] G. Marsaglia and W. Tsang. A simple method for generating gamma variables. ACM Transactions on Mathematical Software, 26(3):363-372, 2000.
[3] J. H. Ahrens and U. Dieter. Computer methods for sampling from gamma, beta, Poisson, and binomial distributions. Computing, 12(3):223-246, 1974.
[4] R. C. H. Cheng and G. M. Feast. Some simple gamma variate generators. Computing, 28(3):290-295, 1979.
[5] D. J. Best. A note on gamma variate generators with shape parameters less than unity. Computing, 30(2):185-188, 1983.

Weighted Approximately Ranked Pairwise loss (WARP)

This entry was posted in Collaborative Filtering IR Research in General on by

Definition
To focus more on the top of the ranked list, where the top \( k \) positions are those we care about using the precision at \( k \) measure, one can weigh the pairwise violations depending on their position in the ranked list. For pair-wise learning procedure, we construct a set of all positive labelled instances, denoted as \(\mathcal{C}_{u}^{+}\)and a set of negative labelled instances as \(\mathcal{C}_{u}^{-}\). The loss is defined as:
\[
\begin{align}
\mbox{err}_{\mbox{WARP}}(\mathbf{x}_{i}, y_{i}) = L[rank(f(y_{i} \, | \, \mathbf{x}_{i}))]
\end{align}
\]where \( rank(f(y_{i} \, | \, \mathbf{x}_{i})) \) is a function to measure how many negative labelled instances are “wrongly” ranked higher than this positive example \( \mathbf{x}_{i} \):
\[
\begin{align}
rank(f(y_{i} \, | \, \mathbf{x}_{i})) = \sum_{(\mathbf{x}^{\prime}, y^{\prime}) \in \mathcal{C}_{u}^{-}} \mathbb{I}[f(y^{\prime} \, | \, \mathbf{x}^{\prime}) \geq f(y \, | \, \mathbf{x}_{i})] \nonumber
\end{align}
\]where \( \mathbb{I}(x) \) is the indicator function, and \( L(\cdot) \) transforms this rank into a loss:
\[
\begin{align}
L(r) = \sum_{j=1}^{r} \tau_{j}, \mbox{with} \; \tau_{1} \geq \tau_{2} \geq \cdots \geq 0.
\end{align}
\]Different choices of \( \tau \) define different importance of the relative position of the positive examples in the ranked list. In particular:

  • For \( \tau_{i} = 1 \) for all \( i \) we have the same AUC optimization as margin ranking criterion.
  • For \( \tau_{1} = 1 \) and \( \tau_{i > 1} = 0 \) the precision at \( 1 \) is optimized.
  • For \( \tau_{i \leq k} = 1 \) and \( \tau_{i > k}=0 \) the precision at \( k \) is optimized.
  • For \( \tau_{i} = 1/i \) a smooth weighting over positions is given, where most weight is given to the top position, with rapidly decaying weight for lower positions. This is useful when one wants to optimize precision at \( k \) for a variety of different values of \( k \) at once.

The loss discussed above is also equal to:
\[
\begin{align}
\mbox{err}_{\mbox{WARP}}(\mathbf{x}_{i}, y_{i}) &= L[rank(f(y_{i} \, | \, \mathbf{x}_{i}))] \times 1\nonumber \\
&= \frac{L[rank(f(y_{i} \, | \, \mathbf{x}_{i}))] \sum_{(\mathbf{x}^{\prime}, y^{\prime}) \in \mathcal{C}_{u}^{-}} \mathbb{I}[f(y^{\prime} \, | \, \mathbf{x}^{\prime}) \geq f(\mathbf{x}_{i})]}{rank(f(\mathbf{x}_{i}))} \nonumber \\
&= \sum_{(\mathbf{x}^{\prime}, y^{\prime}) \in \mathcal{C}_{u}^{-}} \frac{L[rank(f(y_{i} \, | \, \mathbf{x}_{i}))] \mathbb{I}[f(y^{\prime} \, | \, \mathbf{x}^{\prime}) \geq f(\mathbf{x}_{i})]}{rank(f(y_{i} \, | \, \mathbf{x}_{i}))}
\end{align}
\]with the convention \( 0/0=0 \) when the correct label \( y \) is top-ranked. Given a label \( y \) from the positive set, the \(rank\) function essentially is the total number of labels from the negative set which violate the functional relationships. The probability of one negative label to be drawn, given a particular positive label, is:
\[
\begin{align}
P((y^{\prime}, \mathbf{x}^{\prime}) \, | \, (y_{i}, \mathbf{x}_{i})) = \frac{1}{rank(f(y_{i} \, | \, \mathbf{x}_{i}))}
\end{align}
\]Due to the discrete nature of identity functions, we can always replace them with hinge loss:
\[
\begin{align}
\mathbb{I}[f(y^{\prime} \, | \, \mathbf{x}^{\prime}) \geq f(y_{i} \, | \, \mathbf{x}_{i})] \approx \max(0, 1 – f(y_{i} \, | \, \mathbf{x}_{i}) + f(y^{\prime} \, | \, \mathbf{x}^{\prime}))
\end{align}
\]

Online Learning to Rank
The overall risk we want to minimize is:
\[
\begin{align}
Risk(f) = \int \hat{\mbox{err}}_{\mbox{WARP}}(\mathbf{x},y) dP(\mathbf{x},y)
\end{align}
\]An unbiased estimator of this risk can be obtained by stochastically sampling in the following way:

  1. Sample a positive pair \( (\mathbf{x},y)\) according to \( P(\mathbf{x},y) \).
  2. For the chosen \( (\mathbf{x},y) \) sample a negative instance \((\mathbf{x}^{\prime},y^{\prime})\) such that \(1+f(y^{\prime} \, | \, \mathbf{x}^{\prime}) > f(y \, | \, \mathbf{x})\).

This chosen negative instance as well as the positive instance has the contribution:
\[
\begin{align}\label{eq:warp_single_contribution}
L[rank(f(y \, | \, \mathbf{x}))] \max(0,1 – f(y \, | \, \mathbf{x}) + f(y^{\prime} \, | \, \mathbf{x}^{\prime}))
\end{align}\]to the total risk, i.e. taking the expectation of these contributions approximates the risk because we have probability \( \frac{1}{rank(f(y \, | \, \mathbf{x}))} \) of drawing \( (\mathbf{x}^{\prime}, y^{\prime}) \) in step 2 above (Remember that the \( rank \) function is essentially to approximate the total number of violating negative instances). This might suggest that we can perform a stochastic update over parameters.

For large dataset, the stochastic optimization steps discussed above is inefficient:

  1. In step (2) above, we need to compute \( f(y^{\prime} \, | \, \mathbf{x}^{\prime})\) for all possible negative instances.
  2. In single contribution ??, we need to calculate $rank$ function, which also requires to compute $f$ for negative instances.

Some approximation can be used. For step (2), we can sample labels with replacement until we find a violating label.

Now if there are \( k = rank(f(y\, | \, \mathbf{x})) \) violating labels, we use random variable \( N_{k} \) to denote the number of trials in the sampling step to essentially obtain an violating label. This random variable follows a geometric distribution of parameter as (here, the assumption is that the probability to sample the first negative label equals the probability to sample a negative label):
\[
\begin{align}
\frac{k}{Y-1}
\end{align}
\]where \( Y \) is the total number of negative labels. Thus, we have \( k=\frac{Y-1}{\mathbb{E}[N_{k}]} \). This suggests that the value of the $rank$ function may be approximated by:
\[
\begin{align}
rank(f(y \, | \, \mathbf{x})) \approx \left \lfloor \frac{Y-1}{N} \right \rfloor
\end{align}
\]where \( N \) is the number of trials in the sampling.

References:
[1] Jason Weston, Samy Bengio, and Nicolas Usunier. Large scale image annotation: learning to rank with joint word-image embeddings. Machine Learning, 81(1):21–35, October 2010.
[2] Nicolas Usunier, David Buffoni, and Patrick Gallinari. Ranking with ordered weighted pairwise classification. In Proceedings of the 26th Annual International Conference on Machine Learning, ICML ’09, pages 1057–1064, New York, NY, USA, 2009. ACM.

SIGIR 2012 Recap 4

This entry was posted in Research in General on by

SIGIR 2012 was held in Portland, Oregon last week. I attended the conference and found it very interesting and delightful. Let me recap the conference and interesting papers in this short post.

This year, one of the main themes in SIGIR mentioned many times by different people is how to evaluate IR models effectively. Two tutorials dedicated to evaluation method and many more papers are talking about this topic. The one presented by Don Metzler and Oren Kurland in the morning is more towards basic research methods and how to design a reasonable experimental method to validate any ideas. The slides are here. Although the tutorial is basic stuff, it remains valuable as it is the most important part in any research paper and it can go wrong easily. The afternoon tutorial presented by Emine Yilmaz, Evangelos Kanoulas and Ben Carterette are more advanced as it dealt with user models and evaluation metrics. More specifically, the tutorial gave a clear explanation of nearly all evaluation methods and their corresponding user models and sought more depth on the topic. One thing I felt disappointing is that all tutorials focus on static analysis of evaluation methods and off-line evaluations. It would be nice that more on-line evaluation methods can be mentioned and the bridge between two paradigms can be discussed.

I really enjoy the first keynote from this year’s Salton Award winner Norbert Fuhr, entitled “Information Retrieval as Engineering Science”. The basic argument Norbert wanted to make is that IR should base on provable and constructive theories where current IR research seems ignore them at all. He had an provoking example to compare building bridges and building search engines. For bridges, given a certain knowledge of the span and the location and maybe other factors (e.g., budget), engineers can build one single bridge that has nice engineering properties such as beauty and endurance. While on the search engine part, the story is quite different. You probably need to build several search engines or prototypes to have a good feeling of which architecture should be used and what features might be relevant. You even run several systems simultaneously and do A/B testing to determine which one should remain. There’s no theory behind it. However, Norbert didn’t provide any clue on how to obtain such theories.

In regular paper sessions, here’re an incomplete take of what I think is interesting:

The best paper award goes to: Time-Based Calibration of Effectiveness Measuresby Mark D Smucker (University of Waterloo), Charles L. A. Clarke (University of Waterloo) and best student paper award goes to: Top-k Learning to Rank: Labeling, Ranking and Evaluation by Shuzi Niu (Institute of Computing Technology, CAS) Jiafeng Guo Yanyan Lan (Chinese Academy of Sciences) Xueqi Cheng (Institute of Computing Technology, CAS)

Maximum Likelihood as Minimize KL-Divergence 8

This entry was posted in Research in General on by

When I study Product of Experts and Restricted Boltzmann Machine recently, I have found a very interesting technical point to be demonstrated. That is maximum likelihood estimation can be viewed as a process to minimize a KL-Divergence between two distributions.

We start from a simple notation. Let \( P(x_{i} \, | \, \boldsymbol{\Theta})\) be the distribution for generating each data point \( x_{i} \). We can define the model parameter distribution as:
\begin{equation}
P_{\boldsymbol{\Theta}}(x) = P(x \, | \, \boldsymbol{\Theta})
\end{equation}We define the following distribution as the “empirical data distribution”:
\begin{equation}
P_{D}(x) = \sum_{i=1}^{N} \frac{1}{N}\delta(x – x_{i})\label{eq:data_distribution}
\end{equation}where \(\delta\) is the Dirac delta function. We can verify that this is a valid distribution by summing over all \( x\): \(\sum_{j=1}^{N}P_{D}(x_{j}) = 1\). By using this empirical data distribution, we wish to calculate the following KL divergence:
\begin{align}
\mathrm{KL}[ P_{D}(x) \, || \, P_{\boldsymbol{\Theta}}(x)] &= \int P_{D}(x) \log \frac{P_{D}(x)}{P_{\boldsymbol{\Theta}}(x)} \, dx \\
&= \int P_{D}(x) \log P_{D}(x) \, dx – \int P_{D}(x) \log P_{\boldsymbol{\Theta}}(x) \, dx \\
&= -H[P_{D}(x)] – \int P_{D}(x) \log P_{\boldsymbol{\Theta}}(x) \, dx \\
&\propto – \Bigr< \log P_{\boldsymbol{\Theta}}(x) \Bigl>_{P_{D}(x)}
\end{align}The last line comes when we drop \(-H[P_{D}(x)]\), which has nothing to do with parameters \(\boldsymbol{\Theta}\) and \(\Bigr< \Bigl>_{P_{D}(x)}\) represents the expectation over \(P_{D}(x)\). If we minimize the left hand side KL divergence, it is equivalent to minimize the negative expectation on the right hand side. This expectation is indeed:
\begin{align}
\Bigr< \log P_{\boldsymbol{\Theta}}(x) \Bigl>_{P_{D}(x)} &= \sum_{x} P_{D}(x) \log P(x \, | \, \boldsymbol{\Theta}) \\
&= \sum_{x} \Bigr[ \frac{1}{N}\sum_{i=1}^{N}\delta(x – x_{i}) \Bigl] \log P(x \, | \, \boldsymbol{\Theta}) \\
&= \frac{1}{N} \sum_{i=1}^{N} \log P(x_{i} \, | \, \boldsymbol{\Theta})
\end{align}This is indeed log likelihood of the dataset.

Notes on “A comparison of logistic regression and naive Bayes”

This entry was posted in Classic Papers Research in General on by

Andrew Y. Ng and Michael I. Jordan had a classic paper on the comparison between logistic regression and naive Bayes. The main contribution of the paper is a theoretical analysis of how logistic regression and naive Bayes might perform and an experimental comparison to support this idea.

Several important points made by the paper. The first is that:

  • The asymptotic error made by logistic regression is no more than that made by naive Bayes (Proposition 1 in the paper).

This conclusion provides a basis for what seems to be the widely held belief that discriminative classifiers are better than generative ones. The main conclusions of the paper is about the sample complexity of both classifiers. Sample complexity is the number of examples needed to approach the asymptotic error. For logistic regression, such sample complexity is:
\[
m = \Omega(n)
\]which means that the sample complexity is linear in \( n \) (Proposition 2 in the paper). For naive Bayes, we have:
\[
m = O(\log n)
\]which means that the sample complexity is logarithmic in \( n \) (Lemma 3 and Corollary 6 in the paper). All these conclusions imply that even though naive Bayes converges to a higher asymptotic error compared to logistic regression, it may also approach it significantly faster — after \( O(\log n) \), rather than \( O(n) \), training examples.

These ideas are discussed in [1]. Are these theoretical analysis always hold in practice? Not very reliable as far as [2] suggested. Note that these conclusions coming after strong assumptions. Nevertheless, they provide some general idea between logistic regression and naive Bayes.

References:

[1] On Discriminative vs. Generative Classifiers: A comparison of logistic regression and Naive Bayes, Andrew Y. Ng and Michael Jordan. In NIPS 14, 2002. [ps, pdf]
[2] Comment on “On Discriminative vs. Generative Classifiers: A Comparison of Logistic Regression and Naive Bayes”. Jing-Hao Xue and D. Michael Titterington. 2008. Neural Processing Letters 28, 3 (December 2008), 169-187. [pdf]

Hack Tweepy to Get Raw JSON 2

This entry was posted in Research in General on by

Tweepy is a popular Python wrapper for Twitter API. Although it provides a lot of useful features where you don’t need to deal with JSON or XML directly, sometimes you would like to store all information you have requested. In other words, you would like to store the raw JSON returned by Tweepy.

For some reason, this feature is not supported by the current version of Tweepy (as of April 4, 2012). So, we need to hack a little bit to get the result. Indeed, this issue was discussed here. The current solution is to add the following code into “parsers.py” of the source code of Tweepy:

1
2
3

class RawJsonParser(Parser):
    def parse(self, method, payload):
        return payload

Therefore, we can call the following code for invoking a new parser with JSON returned:

1
2

from tweepy.parsers import RawJsonParser
api = tweepy.API(auth_handler=auth, parser=RawJsonParser())