How to Generate Gamma Random Variables 4
In this post, I would like to discuss how to generate Gamma distributed random variables. Gamma random variate has a number of applications. One of the most important application is to generate Dirichlet distributed random vectors, which plays a key role in topic modeling and other Bayesian algorithms.
A good starting point is a book by Kroese et al. [1] where detailed discussion about how to generate a number of different random distributed variables. In the book (Section 4.2.6), they list the following methods for Gamma distribution:
- Marsaglia and Tsang’s method [2]
- Ahrens and Dieter’s method [3]
- Cheng and Feast’s method [4]
- Best’s method [5]
Here, we focus on Marsaglia and Tsang’s method, which is used in GSL Library and Matlab “gamrnd” command (you can check this by typing “open gamrnd”).
Gamma Distribution
As there are at least two forms of Gamma distribution, we focus the following formalism of PDF:
![]()
Marsaglia and Tsang’s Method
The algorithm works as follows for ![]() for
for ![]() :
:
- Set
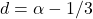 and
and 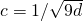 .
. - Generate
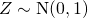 and
and  independently.
independently. - If
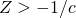 and
and 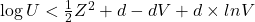 , where
, where 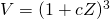 , return
, return 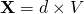 ; otherwise, go back to Step 2.
; otherwise, go back to Step 2.
Two notes:
- This method can be easily extended to the cases where
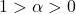 . We just generate
. We just generate 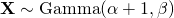 , then
, then 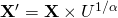 where
where  . Thus,
. Thus, 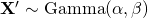 . See details in Page 9 of [2].
. See details in Page 9 of [2]. - For
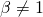 , we firstly generate
, we firstly generate 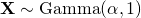 , then
, then 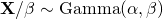 .
.
Implementations
Here, we discuss some implementations details. We start from the original proposed C code from [2]:
#include
extern float RNOR; // Normal random variable
extern float UNI; // Uniform random variable
float rgama(float a) {
float d, c, x, v, u;
d = a - 1. / 3.;
c = 1. / sqrt(9. * d);
for (;;) {
do {
x = RNOR;
v = 1. + c * x;
} while (v <= 0.);
v = v * v * v;
u = UNI;
if (u < 1. - 0.0331 * (x * x) * (x * x)) {
return (d * v);
}
if (log(u) < 0.5 * x * x + d * (1. - v + log(v))) {
return (d * v);
}
}
}
which is slightly different from the algorithm proposed above. Again, this does not handle ![]() and
and ![]() .
.
This is the Matlab sample code from [1]:
function x=gamrand(alpha,lambda)
% Gamma(alpha,lambda) generator using Marsaglia and Tsang method
% Algorithm 4.33
if alpha>1
d=alpha-1/3; c=1/sqrt(9*d); flag=1;
while flag
Z=randn;
if Z>-1/c
V=(1+c*Z)^3; U=rand;
flag=log(U)>(0.5*Z^2+d-d*V+d*log(V));
end
end
x=d*V/lambda;
else
x=gamrand(alpha+1,lambda);
x=x*rand^(1/alpha);
end
This code does everything.
This is the code snippet extracted from GSL library:
double gsl_ran_gamma (const gsl_rng * r, const double a, const double b)
{
/* assume a > 0 */
if (a > 1)
{
double u = gsl_rng_uniform_pos (r);
return gsl_ran_gamma (r, 1.0 + a, b) * pow (u, 1.0 / a);
}
{
double x, v, u;
double d = a - 1.0 / 3.0;
double c = (1.0 / 3.0) / sqrt (d);
while (1)
{
do
{
x = gsl_ran_gaussian_ziggurat (r, 1.0);
v = 1.0 + c * x;
}
while (v >= 0);
v = v * v * v;
u = gsl_rng_uniform_pos (r);
if (u > 1 - 0.0331 * x * x * x * x)
break;
if (log (u) > 0.5 * x * x + d * (1 - v + log (v)))
break;
}
return b * d * v;
}
}
Again, this does everything. Note this code is based on a slightly different PDF: ![]() .
.
Reference
[1] D.P. Kroese, T. Taimre, Z.I. Botev. Handbook of Monte Carlo Methods. John Wiley & Sons, 2011.
[2] G. Marsaglia and W. Tsang. A simple method for generating gamma variables. ACM Transactions on Mathematical Software, 26(3):363-372, 2000.
[3] J. H. Ahrens and U. Dieter. Computer methods for sampling from gamma, beta, Poisson, and binomial distributions. Computing, 12(3):223-246, 1974.
[4] R. C. H. Cheng and G. M. Feast. Some simple gamma variate generators. Computing, 28(3):290-295, 1979.
[5] D. J. Best. A note on gamma variate generators with shape parameters less than unity. Computing, 30(2):185-188, 1983.
