One critical component in Gibbs sampling for complex graphical models is to be able to draw samples from discrete distributions. Take latent Dirichlet allocation (LDA) as an example, the main computation focus is to draw samples from the following distribution:
(1) 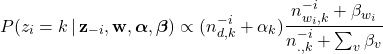
where
So, a straightforward sampling algorithm works as follows:
- Let
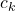 be the right-hand side of Equation \eqref{eq:lda} for topic
be the right-hand side of Equation \eqref{eq:lda} for topic 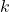 , which is an un-normalized probability.
, which is an un-normalized probability. - We compute the accumulated weights as:
![Rendered by QuickLaTeX.com C[i] = C[i-1] + c_{i} , \,\, \forall i \in (0, K-1]](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-8b939e197d278e87fcb5467d61776f13_l3.png) and
and ![Rendered by QuickLaTeX.com C[0] = c_{0}](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-b5136f6a23d1c4663ace79b4a1e8f4cb_l3.png) .
. - Draw
![Rendered by QuickLaTeX.com u \sim \mathcal{U}(0, C[K-1] )](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-8efafa70d54915b1289f9f356e8c76f8_l3.png) and find
and find 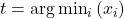 where
where ![Rendered by QuickLaTeX.com x_{i} = C[i] - u](https://www.hongliangjie.com/wp-content/ql-cache/quicklatex.com-30e098e140b71c2a0b65ee9649f2c7d4_l3.png) and
and 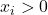
The last line is essentially to find the minimum index that the array value is greater than the random number ![]() .
.
One difficulty to deal with \eqref{eq:lda} is that the right hand side might be too small and therefore overflow (thinking about too many near-zero numbers multiplying). Thus, we want to deal with probabilities in log-space. We start to work with:
(2) ![]()
Notes:
- The log-sampling algorithm for LDA is implemented in Fugue Topic Modeling Package.
- Unless you really face the issue of overflow, sampling in log-space is usually much slower than the original space as log and exp are expensive functions to compute.