Daily Archives: August 17, 2015

Poisson Matrix Factorization 1

This entry was posted in Collaborative Filtering on by

In recent years, Matrix Factorization (MF) methods play a pivotal role in the research of Collaborative Filtering and Recommender Systems. The basic assumption is that, the data can be formed into a N \times M matrix X where N is the number of users and M is the number of items. Each rating X_{i,j} is modeled as a dot-product of the latent factor \theta_{i} for the user i and the latent factor \phi_{j} for the item j. In the classic Probabilistic Matrix Factorization, the rating X_{i,j} is defined as:

(1)   \begin{equation*}X_{i,j} \sim \mathcal{N}(\theta_{i}^{T}\phi_{j}, \sigma^{2})\end{equation*}

where each user factor and each item factor is drawn from another set of Gaussians:

(2)   \begin{align*}\theta_{i} \sim \mathcal{N}(0, \sigma_{U}^{2}I) \\\phi_{j} \sim \mathcal{N}(0, \sigma_{I}^{2}I)\end{align*}

This definition has two issues:

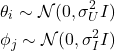
  1. It does not prevent that the ratings become negative, which is a natural result of the Gaussian assumption.
  2. If no heuristics are applied, the model needs to model all zero ratings and therefore, dramatically impacting the predictive performance.

In order to demonstrate the second point, we could see that the log likelihood of the data can be give as:

(3)   \begin{equation*}\log P(X \, | \, \theta, \phi ) = - \frac{1}{2\sigma^{2}} \sum_{i} \sum_{j} ( X_{i,j} - \theta_{i}^{T}\phi_{j})^{2} - \frac{1}{2} N \times M \log \sigma^{2} + C\end{equation*}

where C is a constant. It is obvious that, if X_{i,j} is zero, the model still needs to explain those ratings as well. In [1], the authors just use a variable to indicate whether the rating is observed or not, simply ignoring them, which might be effective, but not justified in the model. In [2], the authors do not ignore unobserved or zero ratings, they put a small confident number for those ratings, a heuristic still.

Recently, Prem Gopalan et al. [3, 4, 5, 6] have proposed a new model called Poisson Factorization (PF) to address these two issues. The central idea is to replace Gaussian assumption with Poisson distribution:

(4)   \begin{equation*}X_{i,j} \sim \mathrm{Poisson}(\theta_{i}^{T}\phi_{j})\end{equation*}

where \theta_{i} and \phi_{j} are drawn from user specific and item specific Gamma distributions. One obvious outcome of this model is that, X_{i,j} are modeled as non-negative values and the latent factors are also non-negative as well. To the second issue mentioned above, we could see the probability of data is：

(5)   \begin{equation*}P(X_{i,j} \, | \, \theta_{i}, \phi_{j}) = (\theta_{i}^{T}\phi_{j})^{X_{i,j}}\frac{\exp \left\{ -\theta_{i}^{T} \phi_{j} \right\}}{X_{i,j}!}\end{equation*}

and therefore, for all items, the log probability is:

(6)   \begin{equation*}\log P(X \, | \, \theta, \phi) = \sum_{i,j} \left\{ X_{i,j}\log \left( \theta_{i}^{T}\phi_{j} \right) - \log X_{i,j}! - \theta_{i}^{T} \phi_{j} \right\}\end{equation*}

As 0!=1, thus, the first term would be zero if X_{i,j} and the second term becomes 1 and thus, only the terms that X_{i,j} would remain. Therefore, as mentioned in the papers, the model, by definition, can support sparse matrices.

Another interesting property of PF, which is mentioned in [5, 6], is that, we can rewrite the Poisson observation model as a two stage process where a user u first decides on a budget b_{u} she has to spend on items, and then spends this budget rating items that she is interested in:

(7)   \begin{align*}b_{u} &\sim \mathrm{Poisson}(\theta_{u}^{T}\sum_{j} \phi_{j}) \nonumber \\[X_{i1},\cdots,X_{iM}] &\sim \mathrm{Multinomial}(b_{u}, \frac{\theta_{u}^{T}\phi_{j}}{\theta_{u}^{T}\sum_{j}\phi_{j}})\end{align*}

This shows that learning a PF model for user-item ratings is effectively the same as learning a budget for each user while also learning how that budget is distributed across items.

Reference

  1. Ruslan Salakhutdinov, Andriy Mnih: Probabilistic Matrix Factorization. NIPS 2007: 1257-1264
  2. Yifan Hu, Yehuda Koren, Chris Volinsky: Collaborative Filtering for Implicit Feedback Datasets. ICDM 2008: 263-272
  3. Prem Gopalan, Laurent Charlin, David M. Blei: Content-based recommendations with Poisson factorization. NIPS 2014: 3176-3184
  4. Prem Gopalan, Francisco J. Ruiz, Rajesh Ranganath, David M. Blei: Bayesian Nonparametric Poisson Factorization for Recommendation Systems. AISTATS 2014: 275-283
  5. Prem Gopalan, Jake M. Hofman, David M. Blei: Scalable Recommendation with Poisson Factorization. CoRR abs/1311.1704 (2013)
  6. Prem Gopalan, Jake M. Hofman, David M. Blei: Scalable Recommendation with Poisson Factorization. UAI 2015.