Smoothing Techniques for Complex Relationships between Probability Distributions

Imagine you want to estimate the probability of how likely a user $u$ in San Francisco would click on a particular news article $i$ . We represent this probability as $P(a_{i} =1 \, | \, u)$ where $a_{i}$ is a binary variable for article $i$ to encode whether the user clicks on it or not. The simplest way to estimate such probability is to stick to Maximum Likelihood Estimation (MLE) where $P$ can be easily computed as:

(1) $\begin{equation*}P( a_{i} = 1 \, | \, u ) = \frac{C(i,u)}{N(i,u)}\end{equation*}$

where $C(i,u)$ is the number of times user $u$ clicks on article $i$ and $N(i,u)$ is the number of times article $i$ is shown to the user $u$ .

Everything works fine until we face a new article, let’s say $j$ , that has never shown to the user before. In this case, $C(j, u)$ is effectively zero and we could show the article to the user a couple of times, in hoping of gathering a couple of clicks. However, this is not guaranteed. Moreover, we should be able to estimate $P$ before showing to the user where $N$ is also zero!

In statistical modeling, a common practice for the situation mentioned above is to impose a prior distribution over $P$ where pseudo counts are added to $C$ and $N$ , yielding non-zero ratio of the Equation \eqref{eq:mle}. For example, one could specify a Beta distribution over $P$ where the posterior distribution is another Beta distribution, making the inference straightforward. A thorough study on how these smoothing techniques applying to Information Retrieval has been intensively explored in [1].

The smoothing scenario becomes complicated when multiple related probability distributions get involved. For instance, instead of just estimating how likely a user would click on an article in general, you would be interested in estimating how likely a user would click an article in a particular time of day (e.g., morning or night), or in a particular geographical location (e.g., coffee shop) like $P( a_{i}=1 \, | \, u, t )$ or $P( a_{i} = 1 \, | \, u, g )$ where $t$ and $g$ represent a particular context. Of course, we could use MLE again to infer these probabilities but, in general, they will suffer from even severe data sparsity issues and stronger and smarter smoothing techniques are required.

Given related probabilities like $P (a_{i} = 1 \, | \, u )$ , $P( a_{i}=1 \, | \, u, t )$ and $P( a_{i} = 1 \, | \, u, g )$ , it is not straightforward to define a hierarchical structure to impose a prior distribution over all these distributions. The general idea would be that, they should be smoothed over each other altogether.

Traditionally, smoothing over a complex structure, or usually, when the structure can be defined as a graph, is a well-studied sub-area of machine learning called Graph-based Semi-Supervised Learning (SSL). Good references are like [2,3]. One example of how such algorithms can be applied to probability distributions is [4]. In general, we perform the following two steps to conduct SSL:

Construct a graph for quantities we care about, in this case, they are probability distributions.
Perform a specific form of label propagation on the graph, resulting in a stationary values of quantities we care about.

However, one critical issue with [2,3,4] is that, the fundamental algorithm is designed based on square errors, assuming Gaussian models underneath, which is not appropriate for probability distributions.

A recently proposed framework nicely tackled the problem mentioned above [5], which is to learn probability distributions over a graph. Let’s list the main framework from the paper:

(2) $\begin{equation*}\mathcal{C}_{KL} = \sum_{i=1}^{l} D_{KL} (r_{i} || p_{i}) + \mu \sum_{i=1}^{m} \sum_{j \in \mathcal{N}_{i}} w_{ij} D_{KL}(p_{i} || p_{j}) - \nu \sum_{i=1}^{m}H(p_{i})\end{equation*}$

where $r_{i}$ is the original probability distributions, $p_{i}$ is the smoothed probability distribution, $D_{KL}$ is the standard KL divergence between two distributions and $H$ is Shannon entropy. Here, $\mu$ and $\nu$ are two hyper-parameters. $l$ is the number of labeled nodes, $m$ is the number of all nodes. Equation \eqref{eq:kl} is a general framework to learn distributions over labeled and unlabeled nodes. The first term imposes the closeness between smoothed version and the original version of distributions and the second term is the smoothness over the neighborhood graph and the third term is to penalize shape distributions, encouraging uniform distributions.

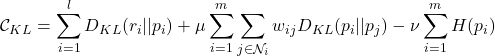
In paper [5], the authors proposed alternative minimization techniques and also mentioned methods of multipliers to solve the problem.

Reference

Chengxiang Zhai and John Lafferty. 2001. A study of smoothing methods for language models applied to ad-hoc information retrieval. In Proceedings of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’01). ACM, New York, NY, USA, 334-342.
D. Zhou, O. Bousquet, T.N. Lal, J. Weston and B. Schölkopf. Learning with Local and Global Consistency. Advances in Neural Information Processing Systems (NIPS) 16, 321-328. (Eds.) S. Thrun, L. Saul and B. Schölkopf, MIT Press, Cambridge, MA, 2004.
Xiaojin Zhu, Zoubin Ghahramani, and John Lafferty. Semi-supervised learning using Gaussian fields and harmonic functions. In The 20th International Conference on Machine Learning (ICML), 2003.
Qiaozhu Mei, Duo Zhang, and ChengXiang Zhai, A General Optimization Framework for Smoothing Language Models on Graph Structures. in Proceedings of the 31th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’08), pp. 611-618, 2008.
Amarnag Subramanya and Jeff Bilmes. 2011. Semi-Supervised Learning with Measure Propagation. The Journal of Machine Learning Research 12 (November 2011), 3311-3370.

Hong, LiangJie

Director of Engineering – AI at LinkedIn Corporation

Director of Engineering – AI at LinkedIn Corporation

Smoothing Techniques for Complex Relationships between Probability Distributions

Reference

Leave a comment