Unbiased Offline Evaluation Process of Contextual Multi-armed Bandit Models 2

This entry was posted in Research in General on by

In this post, I would like to discuss some strategies to evaluate contextual multi-armed bandit (cMAB) models in an unbiased offline evaluation setting. The setting is not only applicable for cMAB models but also can be served as a standard process for any machine learning models from online feedback data.

Review of Contextual Multi-armed Bandit Problems

A cMAB problem is a sequential decision making process. Bandit problems invovle making a decision in each round. Once a decision is made an observation is collected and the corresponding reward computed. The contextual-bandit formalism generalizes this classic setting by introducing contextual information in the interaction loop.

Formally, we define by \mathcal{A} = \{1,2,\cdots, K\}, a set of actions, a contextual vector \mathbf{x}_{t} \in \mathcal{X}, a reward vector \mathbf{r}_{t} = \{\mathbf{r}_{t,1}, \cdots, \mathbf{r}_{t,K}\}, where each \mathbf{r}_{t,a} \in [0,1] and a policy \pi : \mathcal{X} \rightarrow \mathcal{A}. A contextual bandit describes a round-by-round interaction between a learner and the environment. At each round t, the problem can be decomposed into following steps:

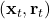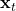  • The environment chooses (\mathbf{x}_{t}, \mathbf{r}_{t}) from some unknown distribution \mathbb{D}. Only \mathbf{x}_{t} is revealed to the learner while the reward is not.
  • Upon observing 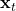\mathbf{x}_{t}, the learner uses some policy 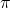\pi to choose an action 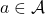a \in \mathcal{A}, and in return observes the corresponding reward \mathbf{r}_{t,a}.
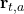  • (Optional) The policy 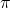\pi is revised with the data collected for this round.

Here, we define \pi is parameterized by an unknown parameter \theta. Ideally, we would like to choose the policy maximizing the expected reward:

    \begin{align*}\arg\max_{\pi} \mathbb{E}_{\mathbf{x}, \mathbf{r} \sim \mathcal{D}} \Bigr[ \mathbf{r}_{\pi(\mathbf{x};\theta)}\Bigl]\end{align*}

An important fact in cMAB is that, only rewards of the chosen actions are observed. An online learning must therefore find a good balance between exploration and exploitation, a challenge in bandit problems. For offline policy evaluation, such partial observation raises even further difficulties. Data in a contextual bandit is often in the form of \mathbf{x}, a, \mathbf{r}_{a}, where a is the action chosen for context x when collecting the data, and \mathbf{r}_{a} is the corresponding reward. If this data is used to evaluate policy \pi, which chooses a different action \pi(x) \neq a, then we simply do not have the reward signal to evaluate the policy in that context.

Policy Evaluation

In order to evaluate different policies in an unbiased environment, we need to gather data using a logging policy. This policy is specially designed such that the data can be re-use for offline evaluation. As pointed out in [1], a randomized data collection, which has been known to be critical condition for drawing valid causal conclusions. From [1], the authors proposed the following data collection procedure. At each round,

  • Environment chooses 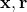\mathbf{x}, \mathbf{r}, i.i.d. from some unknown distribution 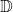\mathbb{D}, and only reveals context \mathbf{x}.
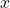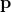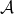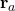  • Based on x, one compute a multinomial distribution \mathbf{p} over the actions \mathcal{A}. A random action a is drawn according to the distribution, and the corresponding reward \mathbf{r}_{a} and probability mass 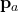\mathbf{p}_{a} are logged. Note that 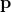\mathbf{p} may depend on \mathbf{x}.

A key point here is that, rather than choosing the optimal action at each round, we would like to choose a random action according some distribution over actions. Also, the probability to select such action should be recorded.

At the end of the process, we have a dataset \mathcal{D} containing data of the form ( \mathbf{x}, a, \mathbf{r}_{a}, \mathbf{p}_{a} ). In statistics, the probabilities \mathbf{p}_{a} are also known as propensity scores.

In order evaluate the value of a policy \pi in such dataset, the following estimator is used:

(1)   \begin{align*}\hat{V}_{\mbox{offline}}(\pi) = \sum_{(x,a,\mathbf{r}_{a},\mathbf{p}_{a}) \in \mathcal{D}} \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}}\end{align*}

This evaluation method is also used in [2] and [3].

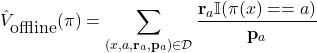
Unbiased Offline Evaluation

We define the value of a policy \pi as:

(2)   \begin{align*}V(\pi) &= \mathbb{E}_{(x,d) \in \mathbb{D}}\Bigr[ \mathbf{r}_{a} P(\pi(x) = a \, |\, x) \Bigl] \\&= \int_{(x,r) \in \mathbb{D}} \mathbf{r}_{a} P(\pi(x) = a \, |\, x) P(x,r) \, dx dr\end{align*}

When the policy is deterministic, meaning that, given a contextual vector x, the arm a is always chosen, the above value becomes:

(3)   \begin{align*}V(\pi) &= \mathbb{E}_{(x,d) \in \mathbb{D}}\Bigr[ \mathbf{r}_{\pi_{x}} \Bigl] \\&= \int_{(x,r) \in \mathbb{D}} \mathbf{r}_{\pi_{x}} P(x,r) \, dx dr\end{align*}

In both cases, we want to prove:

(4)   \begin{align*}\mathbb{E}_{\mathcal{D} \in \mathbb{D}} \Bigr[ \hat{V}_{\mbox{offline}}(\pi)\Big] = V(\pi)\end{align*}

In the following discussion, we focus on the deterministic case. Let us expand the left hand side as:

(5)   \begin{align*}\int_{\mathcal{D} \in \mathbb{D}} \Bigr[ \sum_{(x,a,\mathbf{r}_{a},\mathbf{p}_{a}) \in \mathcal{D}} \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}} \Bigl] P(\mathcal{D}) \, d\mathcal{D}\end{align*}

The important step in the proof is that we need to make use of the following quantity:

(6)   \begin{align*}\mathbb{E}_{a \in \mathbf{p}} \Bigr[ \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}} \Bigl] = \mathbf{r}_{a} \mathbb{I}(\pi(x) == a) = \mathbf{r}_{\pi(x)} \end{align*}

Thus, on expectation, we have:

(7)   \begin{align*}\int_{\mathcal{D} \in \mathbb{D}} \Bigr[ \sum_{(x,a,\mathbf{r}_{a},\mathbf{p}_{a}) \in \mathcal{D}} \frac{\mathbf{r}_{a} \mathbb{I}(\pi(x) == a)}{\mathbf{p}_{a}} \Bigl] P(\mathcal{D}) \, d\mathcal{D} = \int_{\mathcal{D} \in \mathbb{D}} \Bigr[ \sum_{(x, \mathbf{r}) \in \mathcal{D}} \mathbf{r}_{\pi(x)} \Bigl] P(\mathcal{D}) \, d\mathcal{D}\end{align*}

As (x,r) from \mathcal{D} are sampled from \mathbb{D} i.i.d., \mathcal{D} is a random sample from \mathbb{D}. The integral also mounts to \mathbb{D}. Note that the key part is Equation \eqref{randomarm} we need to select arms stochastically.

References

  1. L. Li, S. Chen, J. Kleban, and A. Gupta. Counterfactual estimation and optimization of click metrics for search engines. Technical Report MSR-TR-2014-32, Microsoft Research, 2014.
  2. L. Li, W. Chu, J. Langford, and X. Wang. Unbiased offline evaluation of contextual-bandit-based news article recommendation algorithms. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, WSDM ’11, pages 297–306, New York, NY, USA, 2011. ACM.
  3. A. L. Strehl, J. Langford, L. Li, and S. Kakade. Learning from logged implicit exploration data. In NIPS, pages 2217–2225, 2010.

Leave a comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.

2 thoughts on “Unbiased Offline Evaluation Process of Contextual Multi-armed Bandit Models”

  • Jikai

    Hi,

    I have a question about the data gathering: the performance/user experience, etc will be affected when randomly choosing an action, right? How is this handled?

    Thanks